아이들에게 아직 어려울 수 있는 무한대라는 수학개념을 스토리텔링을 통해 재미있게 풀어서 설명해주는 그림책 “무한대를 찾아서“를 읽으면서 무한대가 무엇인지 어렴풋이 이해했다면, 이번엔 그림책 놀이로 뫼비우스의 띠를 만들어 놀면서 무한대와 친해져 볼까요? ^^
그림책 소개
빨간 새 구두를 선물 받은 날 밤 너무나 신나고 설레이는 여덟살 꼬마 아가씨 우마. 빨리 학교에 가서 새 구두 자랑할 생각에 설레어서 잠이 오지 않아요. 그래서 새 구두 조심스레 신고 잔디밭에 나갔다가 문득 바라 본 밤하늘을 잔뜩 수놓은 별들을 보며 우마의 호기심에 발동이 걸립니다.
우마는 친구들과 무한대에 대해 이야기도 나눠보고 할머니와 선생님 등 어른들에게도 무한대란 무엇일까 질문을 던져봅니다. 하지만 아직 어린 우마에게 무한대는 알듯 말듯 아리송하기만 해요. 질문을 하면 할 수록 우마의 머릿속은 점점 더 복잡해집니다.
그런데, 집에 돌아온 우마에게 맛있는 저녁을 차려 주시던 할머니가 하루종일 아무도 알아주지 않아서 서운했던 빨간 새 구두를 보시면서 참 예쁘다고 칭찬해 주셨어요.
그 순간 나는 깨달았지요.
할머니를 사랑하는 내 마음이 바로 무한대라는 사실을요.

무한대를 찾아서(원제 : Infinity and Me)
글 케이트 호스포드 | 그림 가비 스비아트코브스카 | 옮김 장미란 | 웅진주니어
(발행 : 2013/10/15)
그림책 이야기 : 무한대, 아이들의 끝없는 호기심을 따라서
“무한대를 찾아서”를 활용한 그림책 놀이
놀이 포인트
1. 뫼비우스의 띠 만들고 자르기 놀이
2. 뫼비우스의 띠로 하트 만들기 놀이
3. 무한대 하면 생각나는 것은?
뫼비우스의 띠 만들고 자르기 놀이
무한대 하면 떠오르는 것. 우마의 똘똘한 친구 사만다가 말했었죠.
“무한대 기호가 떠올라.
8자가 누워서 낮잠 자고 있는 모양이야.
그런 모양의 경주로가 있다면 영원히 돌 수 있을거야.”
누워있는 ‘8’자 모양 뫼비우스의 띠 만들기로 그림책 놀이를 구성해 보았습니다. 무한대라는 개념이 그림책을 읽는 아이들에게 쉽지는 않겠지만 “무한대를 찾아서”를 읽어 본 후, 수학적인 개념 주입보다는 자르고 펼치는 놀이로 아이들과 뫼비우스의 띠 만들기를 시도해 보세요. 놀이를 통해 자연스레 이해할 수 있도록 말이죠.
재료: 종이, 풀, 가위, 자, 색연필
1. 40cm 길이의 띠를 여러 장 잘라 준비합니다.

2. 한쪽을 180도(=한번) 비틀어 이어 붙여줍니다. 띠 하나는 비틀지 않고 그대로 붙여주세요.

한 번 꼬아 붙인 띠와 그냥 이어붙인 띠의 모양이 어떻게다른지 비교하기 위해 두가지 모양으로 만들었습니다.
2. 두개의 띠에 면을 따라 가며 천천히 선을 그어보세요.

3. 내가 그린 선의 모양이 어떻게 그려졌는지 자세히 관찰해 보세요.

한번 꼬아서 만든 뫼비우스의 띠는 안과 바깥쪽 면 모두 선이 그어져 있습니다. 꼬지 않고 만든 띠는 바깥쪽에만 선이 그어져 있는 것을 확인 할 수 있습니다.
뫼비우스의 띠는 중심을 따라 한 바퀴 이동하면 출발한 곳과 정반대의 면에 도착하게 됩니다. 계속 선을 그어 두바퀴를 돌게 되면 처음 출발한 위치로 돌아오게 됩니다. 말로 하면 어렵지만 손으로 직접 그려보면 눈에 보이게 됩니다.
3. 띠를 반으로 잘라 보세요.

4. 자른 띠를 관찰해 보세요.

뫼비우스의 띠의 가운데를 자르면 두번 꼬인 띠가 됩니다. 모양을 잘 잡아 보세요. 무한대 표시처럼 보이죠?
5. 자르기 전 뫼비우스의 띠 모양과 비교해 보세요.

자르기 전의 뫼비우스의 띠와 모양을 비교해 보면 이렇습니다. 자르기 전에는 한번 꼬인 띠 모양이고, 자르고 나면 두 번 꼬인 띠로 변신했고 길이도 두배로 길어져 있습니다.
6. 꼬지 않고 이어준 띠도 잘라 보세요.

꼬지 않고 이은 띠는 그대로 각각의 두개의 띠가 만들어 졌습니다.
7. 뫼비우스의 띠(왼쪽)를 자른 것과 꼬지 않고 이어붙인 띠(오른쪽)를 동시에 놓고 비교해 보세요.

가운데를 잘랐는데 뫼비우스의 띠는 두개로 나뉘지 않았다는 것이 신기하다고 아이들은 이야기 합니다. 잘라 놓고 저도 신기했습니다.^^
8. 가운데를 자른 뫼비우스의 띠의 가운데를 다시 한번 잘라 볼까요?

선이 가늘기 때문에 조심조심 천천히 가운데를 잘라 주세요. 어떤 모양이 나올지 아이와 미리 이야기도 나눠보시구요.
9. 큰 무한대 하나와 작은 무한대 하나가 연결되어 생겨났습니다.

이 선의 가운데로 또 잘라보면 어떤 모양이 생겨날까요? 가위질 솜씨 좋은 아이, 호기심 많은 아이는 이 모양을 한번 더 잘라내는데 도전해 보세요. (무한~~도전!!!)
뫼비우스의 띠로 하트 만들기 놀이
1. 두번 꼬아서 이어준 띠를 만들어줍니다.

한번 비틀고 또 한번 비틀어 이어주면 두 번 꼬인 뫼비우스의 띠가 만들어 집니다.
2. 이번에도 띠의 중앙에 선을 그어 보세요.

한번 꼬아서 만든 뫼비우스의 띠는 안팎으로 모두 선이 그어지는 것과 달리 두번 꼬아 만든 띠는 아무리 돌리면서 선을 그어 보아도 이렇게 선이 한쪽 면에만 그어집니다.
3. 띠의 중앙을 따라 잘라주세요.

어떤 모양이 나올까요? 이번에도 자르는 동안 아이와 서로 예상하는 모양을 이야기 해 보세요.
4. 연결된 두개의 하트 모양이 생겨났습니다.

분명 하나의 고리를 잘랐는데 이어진 두개의 고리가 만들어진다는 점, 그것도 하트 모양이라는 점, 참으로 놀랍네요.^^ 수학일까요? 마술일까요?

노란색 화살표 부분을 눌러 주면 하트 모양이 더 뚜렷하게 보입니다.
5. 연결된 하트 모양 띠의 중앙을 따라 또 한번 잘라 보면 어떤 모양이 나올까요?
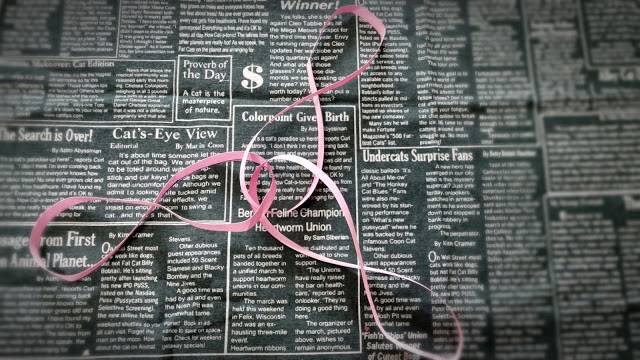
중간이 연결된 3개의 무한대가 생겨났습니다. 또 가운데를 자르면 어떤 모양으로 변신을 할까요? 이 놀이 자체만으로도 무한대 이야기가 하나 더 생겨 날 듯 합니다.^^
무한대 하면 생각나는 것은?
뫼비우스의 띠를 잘라 만든 무한대 띠를 스케치북에 붙이고, 우리 주변 무한대인 것을 찾아서 써보세요.

저는 ‘무한대’ 하면 애니메이션 토이스토리에서 버즈라이트이어가 하늘을 날려고 시도할 때마다 “To Infinity and Beyond!”(무한 공간 저 너머로…!)라고 소리 친 것이 생각납니다. ^^

재활용 마크는 1970년 Gary Anderson(미국)이 처음 디자인했다고 합니다. 정적인 것과 동적인 것을 동시에 표현함으로써 끝없이 순환된다는 뜻을 담기 위해 뫼비우스의 띠를 디자인에 응용했다고 합니다.
‘아는만큼 보인다’는 말대로 알면 알수록 보이는 것들도 더 많이 생겨나는 것 같습니다. 아이들과 뫼비우스의 띠를 활용해 재미있게 놀아 보세요! ^^





그림책으로 꿈찾기 ‘수학자’편에 ‘무한대를 찾아서’로 수업할 예정인데 ‘뫼비우스 띠와 놀자’활동을 계획했어요.
제가 준비한 것보다 종류가 풍성해서 도움받습니다~!
재미있게 몰입할 것 같아요~!
감사합니다^^
아이들과 놀이 수업, 왁자지껄 즐겁고 떠들썩한 풍경이 눈에 그려지는 것 같네요.^^
반갑습니다. 김은신님!
안녕하세요! 저는 강원도의 한 초등학교 교사입니다. 정성껏 작성하신 이 글과 사진 자료를 수업용으로 활용해도 괜찮은지요? seonju.lee@gaonbit.kr로도 문의 메일을 넣어놓았습니다. 답글을 달아주시면 정말 감사하겠습니다!
박종규 선생님, 반갑습니다!
보내주신 메일에 답변 드렸습니다.
아이들과 함께 유익하고 즐거운 시간 보내세요!
경상남도 작은 도시의 작은 마을 도서관에서 그림책놀이를 하고 있는 사람입니다. 선생님의 수업
이야기를 활용해도 되는지 여쭈어봅니다.
박정휘 선생님 반갑습니다!
경상남도 작은 도시 어딜까요? 궁금합니다 ^^
무상으로 활동하고 계시다면 무방합니다.
아이들 모습 공유해주시면 더 좋구요.
아이들과 함께 즐거운 시간 보내세요! ^^
안녕하세요…
저는 체험관에서 근무하는데요.
요즘 아이들과 체험할 자료를 찾는 중에 탐구학습 주제를 “뫼비우스의 띠”로 정했습니다.
자료 찾다가 선생님 글 읽고 이런 내용을 공유해도 되는지 궁금해서요.
주제와 내용 일부를 …
그림책으로 놀기 라는 주제도 좋은 것 같습니다.
좋은 자료 감사합니다.
안녕하세요? 유선희님
체험관에서 무상으로 활동하고 계시다면 공유 가능합니다.
아이들과 즐거운 시간 되시길! ^^
안녕하세요? ^^ 경기도 수원에 중학교에서 중1 학생들 자유학기 지도하고 있습니다. 뫼비우스의 띠 소개하려는데요~ 선생님 자료를 공유해도 될까요? 아이들이 이해하기에 너무 좋은 자료여서요~ 좋은 자료 감사합니다.
송명균 선생님 반갑습니다.
학교 수업에 활용하시는 거라면 공유 가능합니다.
학생들과 알찬 시간 보내세요 ^^